Exercícios

Teorema de Pitágoras

O teorema de Pitágoras é uma expressão matemática que relaciona os lados de um triângulo retângulo, conhecidos como hipotenusa e catetos. Esse teorema não é válido para triângulos acutângulos ou obtusângulos, apenas para os retângulos.

Relações métricas no triângulo retângulo e teorema de Pitágoras

Entre duas torres de 13 m e 37 m de altura existe, na base, uma distância de 70 m. Determine a distância entre os extremos dessa torres. R = 74 m
Em um triângulo retângulo ABC, a diferença entre os catetos é 2 cm e o produto é 48 cm².
Calcule:
a)a hipotenusa deste triângulo. R = 10 cm
b)a altura relativa a hipotenusa. R = 4,8 cm
c)as projeções dos catetos sobre a hipotenusa. R = 6,4 cm e 3,6 cm
Os lados de um losango medem 5 cm e uma das diagonais mede 9,6 cm. Calcule o valor da outra diagonal.
R = 2,8 cm
Num retângulo, um dos lados é 3/4 do outro e a diagonal mede 10 cm. Calcule a área do retângulo. R = 48 cm²
Calcule as medidas dos catetos de um triângulo retângulo, sabendo que a área é 150 m² e que a área do quadrado construído sobre a hipotenusa é 625 m². R = 15 cm e 20 cm
Dado um trapézio ABCD retângulo em A e D, onde AB = 13, CD = 8 e AD = 12. Calcule BC. R = 13 cm
Determine a altura relativa a hipotenusa de um triângulo retângulo sabendo que os catetos medem 3 m e 4 m.
R = 2,4 m
Calcule a medida da diagonal de um quadrado em que o lado mede 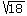. R = 6 cm
Calcule os catetos de um triângulo retângulo, sabendo-se que a razão de suas medidas é 3 : 4 e a hipotenusa mede 15 cm. R = 9 cm e 12 cm
Sabendo que a diferença entre os catetos de um triângulo retângulo ABC é 5 cm e o produto entre eles é 300 cm². Calcule as projeções m e n dos catetos sobre a hipotenusa. R = 9 cm e 16 cm
O perímetro de um triângulo retângulo é 48 cm e a diferença entre as medidas dos catetos é 4 m. Determine a medida do maior cateto. r = 12 m
As diagonais de um losango medem 16 cm e 30 cm. Calcule o valor do lado desse losango. R = 17 cm
Durante um incêndio em um apartamento de edifícios, os bombeiros precisaram usar uma escada magirus de 35 m para atingir a janela do apartamento com incêndio. A escada estava colocada sobre um caminhão a 21
m do edifício. Determine a altura deste apartamento em relação a base da escada. R = 28 m
O triângulo ABC é retângulo em B. Sabendo-se que r = 4 cm e x = 2 cm, calcule os valores dos termos
desconhecidos. R = h =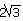 cm, y = 6 cm e s = 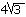cm
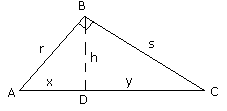
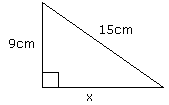
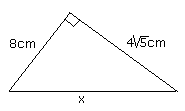
Na figuras abaixo determine os valores desconhecidos.
a) R = 12 cm b) R = 12 cm