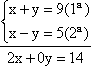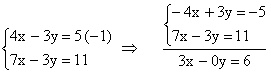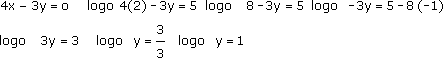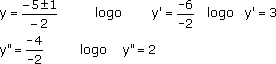Sistemas

Sistemas do 1º grau

 Dizemos que duas equações  do 1º grau,  formam um sistema quando possuem uma solução comum (mesma solução).
Nesse caso as duas equações tem o mesmo conjunto universo.

Resolvendo sistemas do 1º  grau:

1º) Método da adição:          

Esse método consiste em adicionarmos as duas equações membro a membro, observando que nesta operação deveremos eliminar uma variável.

Exemplo 1: 

1º somamos as duas equações membro a membro:

Logo: 2x = 14
logo x = 14/2  Logo x = 7

Voltamos na 1ª ou 2ª equação:
1ª equação:   x + y = 9 (vamos substituir x por 2)
2 + y = 9  logo
y = 9 – 2 logo y = 7
S = {(2;7)} 

Obs: no conjunto solução de um sistema,  devemos colocar o par de números dentro de um parêntesis  por ser um par ordenado, primeiro
x depois y. 

Exemplo 2: 

Observe que na forma em que se encontram as equações. Se adicionarmos não eliminaremos nenhuma das variáveis. Vamos multiplicar a 1ª ou 2ª equação por (-1), para que os coeficientes de y fiquem opostos –3 e +3.

Voltando na 1ª  equação vamos substituir x por 2.

s = {(2;1)}

Sistemas do 2º Grau

Veja os seguintes sistemas de equações, com variáveis x e y.

Note que, em cada sistema temos uma equação do 2º grau e uma equação do 1º grau. Estes são chamados sistemas
do 2º grau.

Resolvendo sistemas do 2º grau:

Vamos resolver pelo método da substituição.

Isolando a variável x na 1ª equação.

x + y = 5    logo  x = 5 – y

Substituímos o valor de x na 2ª equação.

Resolvendo a equação do 2º grau.

Voltando na 1ª equação.
x = 5 – y
x” = 5 – 3   x” = 2
e       x’ = 5 – 2   x’ = 3

S = {(3;2),(2;3)