Regra de três
Grandezas Diretamente e Inversamente ProporcionaisEntendemos por grandeza tudo aquilo que pode ser medido, contado.
Em uma corrida quanto maior for a velocidade, menor será o tempo gasto nessa prova. Aqui as grandezas são a velocidade e o tempo.
Grandezas Diretamente Proporcionais
|
|
Quantidade de gasolina (em litros) |
Quantidade a pagar (em reais) |
|
1 |
0,50 |
|
2 |
1,00 |
|
3 |
1,50 |
Observe:
Se a quantidade de gasolina dobra o preço a ser pago também dobra.
Se a quantidade de gasolina triplica o preço a ser pago também triplica.
Neste caso as duas grandezas envolvidas, quantia a ser paga e quantidade de gasolina, são chamadas grandezas diretamente proporcionais.
Duas grandezas são chamadas, diretamente proporcionais quando, dobrando uma delas a outra também dobra; triplicando uma delas a outra também triplica.
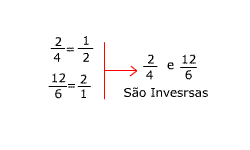
Observe, que as razões são iguais.
![]()
Grandezas inversamente proporcionais
Um professor de matemática tem 24 livros para distribuir entre os seus melhores alunos. Se ele escolher apenas 2 alunos, cada um deles receberá 6 livros. Se ele escolher 4 alunos, cada um deles receberá 6 livros. Se ele escolher 6 alunos, cada um deles receberá 4 livros.
Observe a tabela:
|
Número |
Números |
|
2 |
12 |
|
4 |
6 |
|
6 |
4 |
Se o número de aluno dobra, a quantidade de livros cai pela metade.
Se o número de alunos triplica, a quantidade de livros cai para a terça parte.
Duas grandezas são inversamente proporcionais quando, dobrando uma delas, a outra se reduz para a metade; triplicando uma delas, a outra se reduz para a terça parte… e assim por diante.
Quando duas grandezas são inversamente proporcionais, os números que expressam essas grandezas variam um na razão inversa do outro.
Regra de Três.
Consta na história da matemática que os gregos e os romanos conhecessem as proporções, porem
não chegaram a aplica-las na resolução de problemas.
Na idade média, os árabes revelaram ao mundo a regra de três. Nos século XIII, o italiano Leonardo
de Pisa difundiu os princípios dessa regra em seu livro Líber Abaci, com o nome de Regra de Três Números Conhecidos.
Regra de três simples
Regra de três simples é um processo prático para resolver problemas que envolvam quatro valores dos quais conhecemos três deles. Devemos, portanto, determinar um valor a partir dos três já conhecidos.
Passos utilizados numa regra de três simples
·
Construir uma tabela, agrupando as grandezas da mesma espécie em colunas e mantendo na mesma linha as grandezas de espécies diferentes em correspondência.
·
Identificar se as grandezas são diretamente ou inversamente proporcionais.
·
Montar a proporção e resolver a equação.
Exemplos:
a) Se 8m de tecido custam 156 reais, qual o preço de 12 m do mesmo tecido?

Observe que as grandezas são diretamente proporcionais, aumentando o metro do tecido aumenta na mesma proporção o preço a ser pago.
![]()
Observe que o exercício foi montado respeitando o sentido das setas.
A quantia a ser paga é de R$234,00.
b) Um carro, à velocidade de 60 km/h, faz certo percurso em 4 horas.
Se a velocidade do carro fosse de 80 km/h, em quantas horas seria feito o mesmo percurso?

Observe que as grandezas são inversamente proporcionais, aumentando a velocidade o tempo diminui na razão inversa.
Resolução:
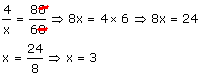
O tempo a ser gasto é 3 horas.
Observe que o exercício foi montado respeitando os sentidos das setas.
Regra de Três Composta
A regra de três composta é utilizada em problemas com mais de duas grandezas, direta ou inversamente proporcionais.
Exemplo:
a) Em 8 horas, 20 caminhões descarregam 160 m3 de areia. Em 5 horas, quantos caminhões serão necessários para descarregar 125 m3?

Aumentando o número de horas de trabalho, podemos diminuir o número de caminhões. Portanto a relação é inversamente proporcional (seta para cima na 1ª coluna).
Aumentando o volume de areia, devemos aumentar o número de caminhões. Portanto a relação é diretamente
proporcional (seta para baixo na 3ª coluna).
Devemos igualar a razão que contém o termo x com o produto das outras razões de acordo com o sentido das setas.
Resolução:
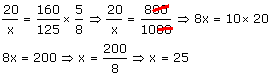
Será preciso de 25 caminhões.


