Progressão aritmética
A Progressão Aritmética (P.A.) é uma sequência de números onde a diferença entre dois termos consecutivos é sempre a mesma. Essa diferença constante é chamada de razão da P.A.
1. (Ita) Uma progressão aritmética ![]() satisfaz a propriedade: para cada
satisfaz a propriedade: para cada ![]() a soma da progressão é igual a
a soma da progressão é igual a ![]() Nessas condições, o determinante da matriz
Nessas condições, o determinante da matriz 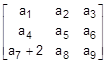 é
é
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
2. (Uerj simulado) Um leão avista uma presa a ![]() metros. No instante em que o leão inicia a perseguição, a presa inicia a fuga. Na mesma linha reta e no mesmo sentido, ambos percorrem as seguintes distâncias, em metros:
metros. No instante em que o leão inicia a perseguição, a presa inicia a fuga. Na mesma linha reta e no mesmo sentido, ambos percorrem as seguintes distâncias, em metros:
|
|
1º segundo |
2º segundo |
3º segundo |
4º segundo |
|
Leão |
|
|
|
|
|
Presa |
|
|
|
|
Admitindo que o padrão de aumento das distâncias percorridas a cada segundo não se altera e desprezando as dimensões dos dois animais, o leão alcança a presa em ![]() segundos.
segundos.
O valor de ![]() é igual a:
é igual a:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
3. (Ifal) Determine o ![]() termo da Progressão Aritmética cujo
termo da Progressão Aritmética cujo ![]() termo é
termo é ![]() e cuja razão é
e cuja razão é ![]()
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
4. (Epcar (Afa)) Constrói-se um monumento em formato de pirâmide utilizando-se blocos cúbicos:
Para a formação piramidal os blocos são dispostos em uma sequência de camadas, sendo que na última camada, no topo da pirâmide, haverá um único bloco, como mostra a figura a seguir.
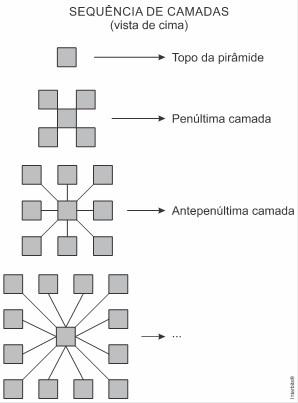
Na disposição total, foram utilizados ![]() blocos, do topo à base da pirâmide.
blocos, do topo à base da pirâmide.
Havendo necessidade de acrescentar uma nova camada de blocos abaixo da base da pirâmide, obedecendo à sequência já estabelecida, serão gastos ![]() blocos nesta camada.
blocos nesta camada.
A quantidade total de divisores positivos do número ![]() é igual a
é igual a
a) ![]()
b) ![]()
c) ![]()
d) ![]()
5. (Ifal) Em um grupo de ![]() crianças, certo número de bombons foi distribuído para cada uma, em uma progressão aritmética crescente, da criança de menor estatura para a de maior estatura. Se colocarmos as crianças nessa ordem, perceberemos que a terceira criança ganhou
crianças, certo número de bombons foi distribuído para cada uma, em uma progressão aritmética crescente, da criança de menor estatura para a de maior estatura. Se colocarmos as crianças nessa ordem, perceberemos que a terceira criança ganhou ![]() bombons e a oitava ganhou
bombons e a oitava ganhou ![]()
Quantos bombons foram distribuídos?
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
6. (Iifal) Ao saber que a esposa estava grávida, um homem passa a armazenar latas de leite no quarto do bebê, aguardando sua chegada, porém, para ficar bem decorado, ele as junta formando uma pirâmide, onde na fila superior tem uma lata, na segunda fila duas latas,
na terceira três e assim por diante até a fila da base. Se ele consegue formar exatamente ![]() filas sem sobras de latas, quantas latas
filas sem sobras de latas, quantas latas
ele conseguiu juntar?
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
7. (Ime) Sejam uma progressão aritmética ![]() e uma progressão geométrica
e uma progressão geométrica ![]() de termos inteiros, de razão
de termos inteiros, de razão ![]() e razão
e razão ![]() respectivamente, onde
respectivamente, onde ![]() e
e ![]() são inteiros positivos, com
são inteiros positivos, com ![]() e
e ![]() Sabe-se, também, que
Sabe-se, também, que ![]()
![]() O
O
valor de ![]() é:
é:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
8. (Ita) Sejam a, b, c e ∈ ℜ. Suponha que ![]() formem, nesta ordem, uma progressão geométrica e que
formem, nesta ordem, uma progressão geométrica e que ![]() formem, nesta ordem, uma progressão aritmética. Então, o valor de
formem, nesta ordem, uma progressão aritmética. Então, o valor de ![]() é
é
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
9. (CPS) O Quadrado Mágico é uma tabela quadrada composta por números inteiros consecutivos a partir do ![]() em que a soma de cada coluna, de cada linha e de cada diagonal são iguais. Essa soma é chamada de número mágico.
em que a soma de cada coluna, de cada linha e de cada diagonal são iguais. Essa soma é chamada de número mágico.
Aprenda a encontrar o número mágico de um quadrado ![]() como o da figura.
como o da figura.
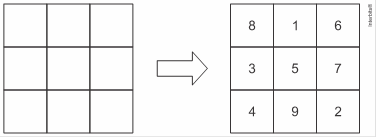
O quadrado mágico ![]() possui
possui ![]() posições, portanto deve ser preenchido com os números de
posições, portanto deve ser preenchido com os números de ![]() até
até ![]() sem repetição.
sem repetição.
O número mágico pode ser encontrado seguindo dois passos.
Passo 1 – Encontrar a soma total dos números. ![]()
Passo 2 – Dividir a soma encontrada pelo número de colunas existentes no quadrado. No caso do quadrado mágico ![]() os
os ![]() números estão agrupados em
números estão agrupados em ![]() colunas. Logo o número mágico será
colunas. Logo o número mágico será ![]()
Em condições semelhantes, o número mágico de um quadrado ![]() será
será
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
10. (Pucsp) Considere a progressão aritmética ![]() crescente, de razão
crescente, de razão ![]() e a progressão geométrica
e a progressão geométrica ![]() decrescente, de razão
decrescente, de razão ![]() de modo que
de modo que ![]() e
e ![]() O valor de
O valor de ![]() é igual a
é igual a
a) ![]()
b) ![]()
c) ![]()
d) ![]()
11. (Pucrj) Os termos da soma ![]() estão em progressão aritmética.
estão em progressão aritmética.
Assinale o valor de ![]()
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
12. (Pucrj) Os números ![]() estão em progressão aritmética (nesta ordem). Quanto vale a soma
estão em progressão aritmética (nesta ordem). Quanto vale a soma ![]()
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
13. (Ifce) Os lados de um triângulo retângulo estão em progressão aritmética. Então, o seno do menor ângulo é
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
14. (Enem 2ª aplicação) Em um trabalho escolar, João foi convidado a calcular as áreas de vários quadrados diferentes, dispostos em
sequência, da esquerda para a direita, como mostra a figura.
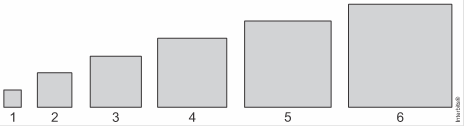
O primeiro quadrado da sequência tem lado medindo ![]() o segundo quadrado tem lado medindo
o segundo quadrado tem lado medindo ![]() o terceiro
o terceiro ![]() e assim por diante. O objetivo do trabalho é identificar em quanto a área de cada quadrado da sequência excede a área do quadrado anterior. A área do quadrado que ocupa a posição
e assim por diante. O objetivo do trabalho é identificar em quanto a área de cada quadrado da sequência excede a área do quadrado anterior. A área do quadrado que ocupa a posição ![]() na sequência, foi representada por
na sequência, foi representada por ![]()
Para ![]() o valor da diferença
o valor da diferença ![]() em centímetro quadrado, é igual a
em centímetro quadrado, é igual a
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
15. (Fac.Albert Einstein – Medicin) Suponha que, em certo país, observou-se que o número de exames por imagem, em milhões por ano,
havia crescido segundo os termos de uma progressão aritmética de razão 6, chegando a ![]() ao final de 10 anos. Nessas condições, o aumento percentual do número de tais exames, desde o ano da observação até ao final do período considerado, foi de
ao final de 10 anos. Nessas condições, o aumento percentual do número de tais exames, desde o ano da observação até ao final do período considerado, foi de
a) ![]()
b) 135%
c) ![]()
d) ![]()
16. (Eear) A progressão aritmética, cuja fórmula do termo geral é dada por ![]() tem razão igual a
tem razão igual a
a) ![]()
b) ![]()
c) ![]()
d) ![]()
17. (Ifal) As medidas dos lados de certo triângulo são expressas por ![]()
![]() e
e ![]() e nessa ordem formam uma progressão aritmética. O perímetro desse triângulo mede
e nessa ordem formam uma progressão aritmética. O perímetro desse triângulo mede
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
18.(Ifsul) A sequência ![]() mantém esse padrão de comportamento para um determinado número de termos
mantém esse padrão de comportamento para um determinado número de termos ![]() A soma destes
A soma destes ![]() termos vale zero.
termos vale zero.
Qual é esse número de termos?
a) ![]()
b) ![]()
c) ![]()
d) ![]()
19. (Ifal) Considere que o número de países que passaram a participar dos Jogos Olímpicos em um dado período de tempo
obedeça à seguinte sequência ![]() que é uma progressão aritmética, então a soma
que é uma progressão aritmética, então a soma ![]() é igual a
é igual a
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
20. (Enem PPL) Um ciclista participará de uma competição e treinará alguns dias da seguinte maneira: no primeiro dia,
pedalará ![]() no segundo dia, a mesma distância do primeiro mais
no segundo dia, a mesma distância do primeiro mais ![]() no terceiro dia, a mesma distância do segundo mais
no terceiro dia, a mesma distância do segundo mais ![]() e, assim, sucessivamente, sempre pedalando a mesma distância do dia anterior mais
e, assim, sucessivamente, sempre pedalando a mesma distância do dia anterior mais ![]() No último dia, ele deverá percorrer
No último dia, ele deverá percorrer ![]() completando o treinamento com um total de
completando o treinamento com um total de ![]()
A distância ![]() que o ciclista deverá pedalar a mais a cada dia, em
que o ciclista deverá pedalar a mais a cada dia, em ![]() é
é
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
GABARITO:
- A; 2. C; 3. C; 4. C; 5. C; 6. C; 7. A; 8. D; 9. C; 10. B; 11. D; 12. E; 13. A; 14. A; 15. B; 16. C; 17. D; 18. C; 19. B; 20. C


