Matrizes
É chamada de matriz uma tabela retangular composta por escalares, onde chamamos estes escalares de entradas ou elementos. Inicialmente, apresentaremos alguns exemplos importantes sobre matrizes de forma generalizada.
1) Determine a matriz A = (aij)3×3 tal que aij = i – j.
2) Construa as seguintes matrizes:
A = (aij)3×3 tal que aij = ![]()
B = (bij)3×3 tal que bij = ![]()
3) Construa a matriz A = (aij)3×2 tal que aij = 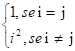
4) Seja a matriz A = (aij)3×4 tal que aij = ![]() , então a22 + a34 é igual a:
, então a22 + a34 é igual a:
5) Determine a soma dos elementos da 3º coluna da matriz A = (aij)3×3 tal que aij = 4 + 3i –i.
6) Determine a soma dos elementos da diagonal principal com os elementos da diagonal secundária da
matriz A = (aij)3×3.
7) Dada a matriz A = (aij)4×4 em que aij = ![]() , determine a soma dos elementos a23 +a34.
, determine a soma dos elementos a23 +a34.
8) Seja a matriz A = (aij)5×5 tal que aij = 5i – 3j. Determine a soma dos elementos da diagonal principal dessa matriz.
9) Determine a soma dos elementos da matriz linha (1×5) que obedece a lei: aij = 2i2 – 7j.
10) Determine a e b para que a igualdade 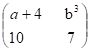 =
= ![]() seja verdadeira.
seja verdadeira.
11) Sejam A = 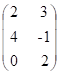 e B =
e B = 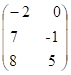 , determine (A + B)t.
, determine (A + B)t.
12) Dadas as matrizes A = ![]() e B =
e B = ![]() , determine x e y para que A = Bt.
, determine x e y para que A = Bt.
13) Resolva a equação matricial: 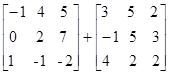 = x +
= x + 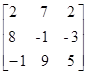 .
.
14) Determine os valores de x e y na equação matricial: ![]() .
.
15) Se o produto das matrizes 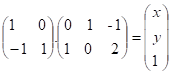 é a matriz nula, x + y é igual a:
é a matriz nula, x + y é igual a:
16) Se ![]() , determine o valor de x + y.
, determine o valor de x + y.
17) Dadas as matrizes A = ![]() B =
B = ![]() e C =
e C = ![]() , calcule:
, calcule:
a) A + B b) A + C c) A + B + C
18) Dada a matriz A = 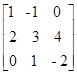 , obtenha a matriz x tal que x = A + At.
, obtenha a matriz x tal que x = A + At.
19) Sendo A = (aij)1×3 tal que aij = 2i – j e B = (bij)1×3 tal que bij = -i + j + 1, calcule A + B.
20) Determine os valores de m, n, p e q de modo que: ![]() .
.
21) Determine os valores de x, y, z e w de modo que: ![]() .
.
22) Dadas as matrizes A = ![]() , B =
, B = ![]() e C =
e C = ![]() , calcule:
, calcule:
a) A – B b) A – Bt – C
23) Dadas as matrizes A = ![]() , B =
, B = ![]() e C =
e C = ![]() , calcule o resultado das seguintes operações:
, calcule o resultado das seguintes operações:
a) 2A – B + 3C b) ![]()
24) Efetue:
a) ![]() b)
b) ![]() c)
c) 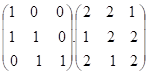
25) Dada a matriz A = 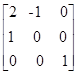 , calcule A2.
, calcule A2.
26) Sendo A = ![]() e B =
e B = ![]() e C =
e C = ![]() , calcule:
, calcule:
a) AB b) AC c) BC


