Geometria analítica – reta

1. (Ueg)  Uma circunferência com centro na origem está tangenciando duas retas paralelas de equações  e  Nesse caso, o valor de  é  

a)    

b)    

c)    

d)    

e)    

  

2. (Efomm)  A projeção ortogonal de  sobre a reta  sabendo-se que  e  terá
as coordenadas da projeção

a)    

b)    

c)    

d)    

e)    

  

3. (Ime)  Sejam os pontos     e  A reta  passa por  e corta o lado  dividindo o pentágono  em dois polígonos de mesma área.
Determine a soma das coordenadas do ponto de interseção da reta  com a reta que liga  e  

a)    

b)    

c)    

d)    

e)    

  

4. (Ifal)  Dados os pontos  e B(0, 4) pertencentes a um sistema de eixos ortogonais num plano, podemos afirmar que:

 

I. A distância entre esses pontos é

II. A equação da reta que passa por esses pontos é

III. A equação da circunferência que tem centro em  e passa por  é

Das afirmativas anteriores, é(são) verdadeira(s)

a) apenas I.   

b) apenas II.    

c) apenas III.    

d) I e II.    

e) II e III.    

  

5. (Pucsp)  A figura mostra um triângulo retângulo  de hipotenusa  com  e

 

 

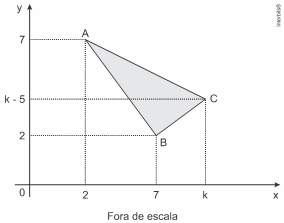
Sabendo que a área do triângulo  é  o valor da abscissa do ponto  é

a)    

b)    

c)    

d)    

  

6. (Fgv)  Os pares  dados abaixo pertencem a uma reta  do plano cartesiano:

 

 

Podemos afirmar que

a) a reta  intercepta o eixo das abscissas no ponto de abscissa    

b) o coeficiente angular da reta  é    

c) a reta  determina com os eixos cartesianos um triângulo de área    

d)  será positivo se, e somente se,    

e) A reta  intercepta o eixo das ordenadas no ponto de abscissa    

  

7. (Uece)  Em um plano, munido do sistema de coordenadas cartesianas usual, as equações  e  representam duas retas concorrentes. A medida da área da região limitada por essas retas e pelo eixo dos  é

Dados:  unidade de área

a)    

b)    

c)    

d)    

  

8. (Ucpel)  Considerando que as três retas no plano  dadas pelas equações   e  interceptam-se num ponto  pode-se afirmar que o valor de  é

a)    

b)    

c)    

d)    

e)    

  

9. (Fgv)  Os pontos de coordenadas cartesianas  e  pertencem a uma circunferência. Uma reta que passa, necessariamente, pelo centro dessa circunferência tem equação

a)    

b)     

c)    

d)    

e)    

  

10.(Upf)  Sobre a figura abaixo, sabe-se que a equação de  é  que os pontos  e  são simétricos em relação ao eixo das abscissas; que as retas  e  são paralelas; e que  é perpendicular a

 

 

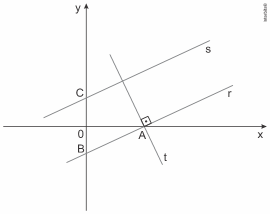
Nessas condições, a equação da reta  é

a)    

b)    

c)    

d)    

e)    

  

11.(Ufjf-pism 3)  Considere os pontos     equação da reta que contém o segmento  a equação da reta que contém o segmento  e o ângulo agudo formado entre elas são, RESPECTIVAMENTE:

a) Impossível    

b)    

c)    

d)    

e)    

  

12. (cftmg)  Sejam as funções reais    e  Considerando todas as interseções entre essas retas, o único quadrilátero que pode ser desenhado, utilizando quatro dessas interseções como vértices, é um

a) losango.
  

b) trapézio.
  

c) quadrado.
  

d) retângulo.
  

  

13. (Unisc)  Os pontos   e  do plano são colineares. O valor de  é igual a

a)    

b)    

c)    

d)    

e)    

  

14. (Ueg)  Na figura a seguir, as retas  são paralelas e seus coeficientes lineares estão em uma progressão aritmética de
razão

 

 

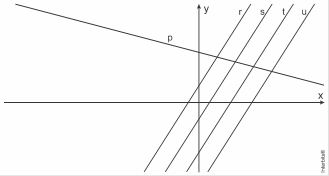
Sabendo-se que a equação da reta  é  e da reta  é  o ponto de intersecção da reta  com reta  é

a)    

b)    

c)    

d)    

e)    

  

15. (Uemg)  No gráfico, representado a seguir, uma das retas esboçadas tem inclinação igual a  e a outra reta,
inclinação igual a  Sabendo-se disso, a área (em unidade de área) da região hachurada é

 

 

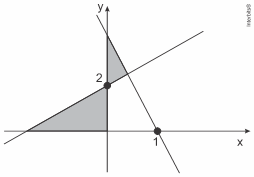
a)    

b)    

c)    

d)    

  

16. (Famema) Em um plano cartesiano, a parábola  e a reta  se intersectam nos pontos  e  A
distância entre esses dois pontos é

a)    

b)    

c)    

d)    

e)    

  

17. (Enem (Libras))  Um sítio foi adquirido por  O proprietário verificou que a valorização do imóvel, após sua aquisição, cresceu em função do tempo conforme o gráfico, e que sua tendência de valorização se manteve nos anos seguintes.

 

 

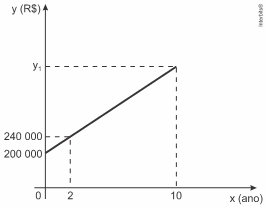
O valor desse sítio, no décimo ano após sua compra, em real, será de

a)    

b)    

c)    

d)    

e)    

  

18. (Uece)  Em um plano, munido do referencial cartesiano usual, seja  o ponto de interseção das retas  e  Se os pontos  e  são respectivamente as interseções de cada uma destas retas com o eixo-x, então, a área do triângulo  é igual  

a)    

b)    

c)    

d)    

  

19. (Ufrgs)  Os pontos  e  determinam um hexágono regular  de lado  tal que o ponto  tem coordenadas  e o ponto  tem coordenadas  como na figura abaixo.

 

 

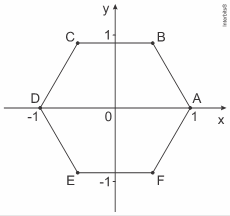
A equação da reta que passa pelos pontos  e  é

a)    

b)    

c)    

d)    

e)    

  

20. (Ita)  Considere a reta  Seja  o vértice de um quadrado  cuja diagonal  está contida em  A área deste quadrado é

a)    

b)    

c)    

d)    

e)    

  

21. (Upe-ssa 3)  No plano cartesiano, a reta   intersecta o eixo das abscissas no ponto  e o eixo das ordenadas no ponto  Nessas condições, qual é a distância entre os pontos  e  

a)    

b)    

c)    

d)    

e)    

  

22. (Unicamp) Considere a circunferência de equação cartesiana  Qual das equações a seguir representa uma reta que divide essa circunferência em duas partes iguais?

a)    

b)    

c)    

d)    

  

23. (Acafe)  Na figura abaixo, a reta  dada pela equação  se intercepta com a reta  no ponto

 

 

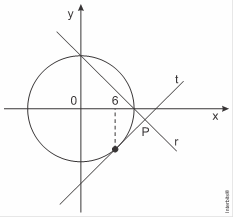
Então, a soma das coordenadas do ponto  é igual a:

a)    

b)    

c)    

d)    

  

24. (Fuvest) Duas circunferências com raios  e  têm centros no primeiro quadrante do plano cartesiano e ambas tangenciam os dois
eixos coordenados. Essas circunferências se interceptam em dois pontos distintos de coordenadas  e
O valor de  é igual a

a)    

b)    

c)    

d)    

e)    

  

25. (Pucsp)  A circunferência  de centro  e a reta  se interceptam nos pontos  e  A área do triângulo  em unidades de área, é

a)    

b)    

c)    

d)    

 

GABARITO: