Geometria analítica – cônicas
As cônicas ou secções cônicas são curvas obtidas pela intersecção de um plano com um cone duplo. De acordo com a inclinação desse plano, a curva será chamada de elipse, hipérbole ou parábola. Quando o plano está paralelo ao plano da base do cone, a curva é uma circunferência sendo considerada um caso particular da elipse.
1.(Espcex (Aman)) Uma elipse tem centro na origem e vértices em 
e 
com 
A área do quadrado inscrito nessa elipse é
a) 
b) 
c) 
d) 
e) 
2. (Uece) No plano, com o sistema de coordenadas cartesianas usual, a equação 
representa
a) uma circunferência.
b) duas retas.
c) uma parábola.
d) uma elipse.
3. (Ime) Seja uma elipse com focos no eixo 
e centrada na origem. Seus eixos medem 
e 
Considere
uma hipérbole tal que os focos da elipse são os vértices da hipérbole e os focos da hipérbole são os vértices da elipse. As parábolas que passam pelas interseções entre a elipse e a hipérbole e que são tangentes ao eixo 
na origem, têm as seguintes equações:
a) 
b) 
c) 
d) 
e) 
4. (Esc.Naval) Seja 
um ponto da elipse 
de focos 
e 
e excentricidade 
Calcule 
e assinale a opção correta.
a) 
b) 
c) 
d) 
e) 
5. (Uece) No plano, com o sistema de coordenadas cartesiano usual, a área do quadrilátero convexo cujos vértices são os pontos de interseção das elipses representadas pelas equações 
e 
é 
a) 
b) 
c) 
d) 
6. (Espcex(Aman)) Os valores reais de 
para os quais a reta 
seja tangente à elipse de equação 
são iguais a
a) 
e 
b) 
e 
c) 
e 
d) 
e 
e) 
e 
7. (Espcex(Aman)) Considere as afirmações:
I. Uma elipse tem como focos os pontos 
e a medida do eixo maior é 
Sua equação é 
II. Os focos de uma hipérbole são 
e sua excentricidade é 
Sua equação é 
III. A parábola 
tem como vértice o ponto 
Com base nessas afirmações, assinale a alternativa correta.
a) Todas as afirmações são falsas.
b) Apenas as afirmações I e III são falsas.
c) Apenas as afirmações I e II são verdadeiras.
d) Todas as afirmações são verdadeiras.
e) Apenas a afirmação III é verdadeira.
8. (Mackenzie) Com relação às equações das elipses 
e 
podemos afirmar que
a) as elipses têm centros coincidentes.
b) as elipses têm a mesma distância focal.
c) as elipses têm a mesma excentricidade.
d) as elipses têm focos sobre o eixo das abscissas.
e) o eixo maior de uma delas é o dobro do eixo menor da outra.
9. (Ifpe) Bira adquiriu uma cabra que pasta em um campo retangular. Para delimitar o gramado, ele pretende traçar uma
elipse inscrita num terreno retangular de 
por 
Para isso, ele deve utilizar um fio esticado preso por duas estacas 
e 
conforme mostra a figura.
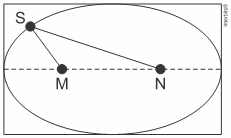
Qual deve ser a distância entre as estacas e 
a)
b) 
c) 
d) 
e) 
10. (Espcex(Aman)) Uma reta 
passa pelo ponto 
e é tangente à parábola de equação 
no ponto 
Assinale a alternativa que apresenta uma solução correta de acordo com essas informações.
a) 
e 
b) 
e 
c) e 
d) 
e 
e) 
e 
11. (Fgv) No plano cartesiano, há dois pontos R e S pertencentes à parábola de equação 
e que estão alinhados com os pontos A(0,3) e B(4,0). A soma das abscissas dos pontos R e S é:
a) -0,45
b) -0,55
c) -0,65
d) -0,75
e) -0,85
12. (Uema) Uma família da cidade de Cajapió – MA comprou uma antena parabólica e o técnico a instalou acima do telhado. A antena projetou uma sombra na parede do vizinho, que está reproduzida abaixo, coberta com uma
folha quadriculada.
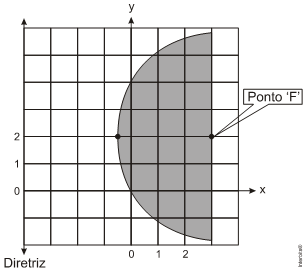
Note que a figura projetada na parede é uma cônica. Considerando as medidas mostradas e o sistema
cartesiano contido na folha quadriculada, a equação que representa a cônica será
a) 
b) 
c) 
d) 
e) 
13. (Ime) Uma elipse cujo centro encontra-se na origem e cujos eixos são paralelos ao sistema de eixos cartesianos possui comprimento da semi-distância focal igual a e excentricidade igual a 
Considere que os pontos 
e 
representam as interseções da elipse com as retas de equações 
e 
A área do quadrilátero 
é
a)
b) 
c) 
d) 
e) 
14. (Espcex (Aman)) Sobre a curva 9x2 + 25y2 – 36x + 50y – 164 = 0, assinale a alternativa correta.
a) Seu centro é (– 2,1).
b) A medida do seu eixo maior é 25.
c) A medida do seu eixo menor é 9.
d) A distância focal é 4.
e) Sua excentricidade é 0,8.
15.(Mackenzie) Dadas as cônicas de equações 
e 
assinale a alternativa INCORRETA.
a) Os gráficos de 
e 
são, respectivamente, uma circunferência e uma elipse.
b) As duas cônicas têm centro no mesmo ponto.
c) As duas cônicas se interceptam em dois pontos distintos.
d) O gráfico da equação é uma circunferência de raio 
e) O gráfico da equação é uma elipse com centro 
16. (Unifor) Uma bola é jogada dentro de uma cesta cuja superfície é obtida girando a parábola em torno do eixo 
O centro da bola ocupa um ponto de altura 
O raio da bola é:
a) 
b) 
c) 
d) 
e) 
17. (Ita) Sobre a parábola definida pela equação 
pode-se afirmar que
a) ela não admite reta tangente paralela ao eixo Ox.
b) ela admite apenas uma reta tangente paralela ao eixo Ox.
c) ela admite duas retas tangentes paralelas ao eixo Ox.
d) a abscissa do vértice da parábola é 
e) a abscissa do vértice da parábola é 
18. (Ufrn) Um arquiteto projetou, para um salão de dimensões 22 m por 18 m, um teto de gesso em formato de elipse com o eixo maior medindo 20 m e o eixo menor, 16 m, conforme ilustra a figura abaixo.
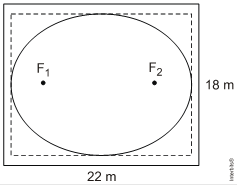
O aplicador do gesso afirmou que saberia desenhar a elipse, desde que o arquiteto informasse as posições dos focos.
Para orientar o aplicador do gesso, o arquiteto informou que, na direção do eixo maior, a distância entre cada foco e a parede mais próxima é de
a) 3 m.
b) 4 m.
c) 5 m.
d) 6
m.
19. (Esc. Naval) A equação 
no plano 
representa
a) duas retas
b) uma circunferência
c) uma elipse
d) uma hipérbole
e) uma parábola
20. (Fgv) Sendo m o maior valor real que x pode assumir na equação analítica 
e n o maior valor real que y pode assumir nessa mesma equação, então, 
é igual a
a) 8.
b) 7.
c) 6.
d) 4.
e) 3.
21. (Udesc) A área delimitada por uma elipse cuja equação é 
é dada por 
Então, a área da região situada entre as elipses de equações 
e 
é:
a) 
b) 
c) 
d) 
e) 
22. (Espcex (Aman)) A representação no sistema cartesiano ortogonal da equação 
é dada por
a) duas retas concorrentes.
b) uma circunferência.
c) uma elipse.
d) uma parábola.
e) uma hipérbole.
23. (Ime) Uma hipérbole de excentricidade 
tem centro na origem e passa pelo ponto 
.
A equação de uma reta tangente a esta hipérbole e paralela a 
é:
a) 
b) 
c) 
d) 
e) 
24. (Uel) O vértice, o foco e a reta diretriz da parábola de equação y = x2 são dados por:
a) Vértice: (0, 0); Foco: (0, 1/4); Reta diretriz y = -1/4
b) Vértice: (0, 0); Foco: (0, 1/2); Reta diretriz y = -1/2
c) Vértice: (0, 0); Foco: (0, 1); Reta diretriz y = -1
d) Vértice: (0, 0); Foco: (0, -1); Reta diretriz y = 1
e) Vértice: (0, 0); Foco: (0, 2); Reta diretriz y = -2
25. (Ufc) O número de pontos de interseção das curvas x2 + y2 = 4 e (x2/15) + (y2/2) = 1 é igual a:
a) 0
b) 3
c) 4
d) 5
e) 6
GABARITO:
1. A; 2. D; 3. E; 4. E; 5. B; 6. A; 7. C; 8. C; 9. D; 10. E; 11. D; 12. A; 13. D;
14. E; 15. C; 16. B; 17. B; 18. C; 19. D; 20. C; 21. C; 22. E; 23. A; 24. A; 25. C
