Geometria

O nome Geometria em grego, significa medida da terra. (geo = terra; metria = medida)

No antigo Egito, a geometria era amplamente utilizada. Os agrimensores usava-na para medir terrenos, enquanto os construtores recorriam  a ela para fazer edificações.  As famosas pirâmides, construídas próximas ao
rio Nilo, são um ótimo exemplo disso

Os Egípcios  ganharam tanta fama que os matemáticos gregos iam constantemente ao Egito em busca de novas aplicações na geometria.

Por volta de 600 a.C, os matemáticos gregos começam a sistematizar os conhecimentos geométrico que foram adquirindo, fazendo com que a Geometria deixasse de ser puramente experimental.

Esse trabalho de organização lógica dos conhecimentos foi feito principalmente pelo matemático grego Euclides, por volta de 300 a.C, e reunido numa obra de 13 volumes, chamada os Elementos.

Toda a geometria que estudamos hoje é praticamente a mesma daquela época.

Ponto,
reta e plano não são definidos. Temos a ideia intuitiva de ponto (quando olhamos uma estrela no céu, localizamos uma cidade no mapa etc…), de reta (observando as linhas do campo de futebol, de uma quadra de futsal os fios da rede elétrica bem esticado etc…),  de plano (observando o piso de sua casa, o campo de futebol a superfície de uma
piscina etc…).

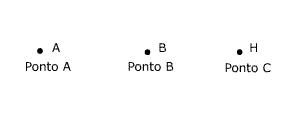
Se observarmos bem a nossa volta,  vamos nos deparar com estes a todo momento. 

Ponto:
Não possui dimensões. Representamos o ponto por uma letra maiúscula do alfabeto latino.

Exemplos:

Reta:
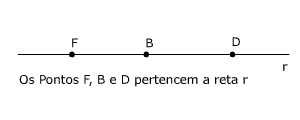
A reta é imaginada sem espessura, não tem começo e nem fim. Representamos a reta por uma letra minúscula  do alfabeto latino, quando desenhamos uma reta no caderno ou quadro, estamos representado parte da reta.

Exemplos:

Plano:
O plano é imaginado como um conjunto infinito de pontos. Plano é imaginado sem limites em todas as direções, como acontece com a reta é impossível representarmos o plano no papel ou quadro. Por isso representamos parte
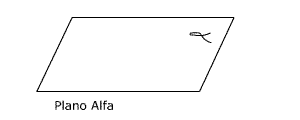
deste. Representamos o plano por uma letra do alfabeto grego. Como alfa(a), beta (b) e gama (g).

Exemplos:

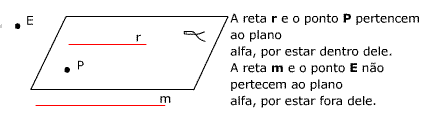
Observe:

Devemos lembrar que, usamos pertence e não pertence para relacionar elemento e conjunto, está contido
e não está  contido  para relacionar conjunto com conjunto.
Vale lembrar que ponto é elemento, reta e plano são conjuntos.

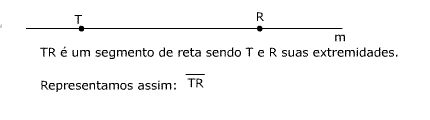
Dados dois pontos distintos(diferentes), a reunião do conjunto  desses dois pontos com o conjunto dos pontos que estão entre eles é um seguimento de reta.

Exemplo:

 Como vimos em geometria, a reta é considerada um conjunto de pontos. Considere um ponto O que pertence a uma reta r. Podemos dizer que esse ponto O separa a reta em dois conjuntos de pontos. Cada um desses
conjuntos de pontos é denominado semi-reta. O ponto O é chamado origem das semi-resta.

Exemplo: