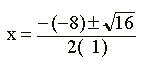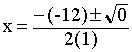Equações do segundo grau

 a  representa o coeficiente de x².

 b  representa o coeficiente de x.

c representa o termo independente. 

Exemplos de equações  do 2º grau. 

5x² – 3x + 2 = 0   onde:  a = 5,  b = – 3 e c = 2 

x² + 6x + 9 = 0     onde:  a = 1,  b = 6 e  c = 9 

-3x² + 7x + 1 = 0 onde:  a = -3, b = 7 e c = 1 

-x² + 5x – 6 = 0   onde: a = – 1,  b = 5 e c = -6 

3x² – 5 = 0         onde: a = 3, b = 0 e c = – 5 

x² + 4x = 0         onde: a = 1, b = 4 e c = 0 

Equações do 2º grau Completas e Incompletas 

Completas: ax² + bx + c = 0 

Quando possui os coeficientes a, b e c. 

Exemplos: 

x² – 4x – 12 = 0, onde: a = 1, b = – 4 e c = -12 

– x² + 11x – 18 = 0, onde: a = -1, b = 11 e c = – 18 

Incompletas: ax² + bx = 0,   ax² + c = 0   ou   ax² = 0 

Quando b ou c é igual a zero, ou ambos iguais a zero. 

Exemplos: 

3x – 4a = 0, onde:
a = 3, b = – 4 e c = 0 

2x² + 5 = 0, onde: a = 2, b = 0 e c = 5 

3x² = 0, onde: a = 3, b = 0 e c = 0 

Raízes de uma equação do 2º grau 

Dizemos que um número é raiz da equação, quando este torna a sentença matemática verdadeira. 

Exemplos: 

1.      Verifique se o número 9 é raiz da equação x² – 11x + 18 = 0. 

x² – 11x + 18 = 0 

(9)² – 11(9) + 18 = 0 (substituímos a variável x por 9) 

81 – 99 + 18 = 0  0 = 0 (sim, 9 é raiz da equação, observe que os dois membros são iguais) 

2.      Verifique se  3 é raiz da equação 2x² + 5x – 3 = 0. 

2x² + 5x – 3 = 0 

2(3)² + 5(3) – 3 = 0 (substituímos a variável x por 3) 

2(9) + 15 – 3 = 0

18 + 15 – 3 = 0

30 ¹ 0 (não, 3 não é raiz da equação, observe que os dois membros são deferentes) 

Resolvendo Equações do 2º Grau 

Equações Incompletas 

·
ax² – bx = 0, (c = 0)

a)x² – 4x = 0 

x(x – 4) = 0 (observe: x foi colocado em evidência) 

x = 0
x – 4 = 0
x = 4
S = {0;4} 

b)-2x² – 8x = 0 

x(-2x – 8) = 0 (observe: x foi colocado em evidência) 

 x = 0 

-2x = 8 (-1)
2x = – 8

x = – 4 

S = {0;-4} 

   Conclusão:
Neste tipo de equação sempre umas das raízes vai ser igual a zero.

·
ax² + c = 0, (b = 0)

a)x² – 16 = 0 

x² = 16 (dois números que elevado ao quadrado dê dezeseis , – 4 e + 4).

x = ±  4 

S = {- 4; 4} 

b)-2x² + 8 = 0  

-2x² = – 8(-1) 

2x² = 8 

x² = 4 

x = ±  2 

S = {- 2; + 2} 

Conclusão: Neste tipo de equação sempre as raízes vão ser opostas.

ax² = 0, (b = 0, c = 0)

5x² = 0 

 
x² = 0

x = 0 (zero é nulo) 

S = { 0 } 

Conclusão: Neste tipo de equação sempre a raiz  vai ser igual a zero. 

Equações Completas 

·
ax² + bx + c = 0 

Usamos a fórmula de Báskara.(Foi um matemático indiano) 

Observe, que a, b e c são os coeficientes da equação do 2º grau.

Resolução

Exemplos: 

x² – 8x + 12 = 0 

a = 1, b = – 8 e c = 12 

(primeiro vamos calcular o valor de delta)

(substituímos a por 1, b por –8 e c por 12) 

 (Delta positivo)

   (fórmula de Baskara) 

(substituímos b por – 8, delta por 16 e a por 1) 

S = {6 ; 2} 

·
x² – 12x + 36 = 0 

 a = 1, b = – 12 e c = 36 

 (Delta igual a zero)

S = {6} 

·
2x² – 4x + 3 = 0

a = 2, b = – 4 e c = 3 

  (Delta negativo) 

S = {  }, não existe raiz de número real negativo 

Importante

D > 0(Positivo)

A equação possui duas raízes reais e diferentes. (x^’ ¹ x^”) 

D < 0 (Negativo)

A equação não possui raízes reais. 

D = 0 

A equação possui duas raízes reais e iguais. (x^’ = x^”) 

Problemas Envolvendo o Discriminante (Delta) 

Exemplo:

Determine o valor de m na equação 2x² + 3x + m, para que as raízes sejam reais e iguais. 

D = 0 (Raízes reais e iguais) 

a = 2, b = 3 e c = m

(Esta equação só vai possuir raízes reais e iguais quando m = 9/8) 

·
Determine o valor de r na equação 2x² – 4x + 5r, para que as raízes sejam reais e diferentes. 

D > 0

a = 2, b = – 4 e c = 5r 

 (quando multiplicamos por – 1 o sinal da desigualdade muda) 

 
(Esta equação só vai possuir raízes reais e diferentes quando r < 2/5)·       

Determine o valor de k na equação -3x² + 5x – 2k, para que não exista raízes  reais. 

D < 0

a = – 3,  b = 5 e c = -2k 

Soma e Produto das Raízes da Equação do 2º Grau 

É possível calcular a soma ou produto das raízes da equação do 2º grau sem precisar resolver a equação. Graças as relações de Girard.

Soma das raízes. 

Produto das raízes. 

Exemplos: 

Calcule a soma e o produto das raízes  equações do 2º grau. 

x² + 7x + 12 = 0 

a = 1,  b = 7 e c = 12 

Determine o valor de m na equação 4x² – (m – 2)x + 3 = 0 para que a soma das raízes seja 3/4.