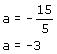Equações do primeiro grau

Equações do 1º grau com uma variável

         Equação é toda sentença matemática aberta representada por uma igualdade, em que exista uma ou mais letras que representam números desconhecidos.

          Exemplo:
X + 3 = 12 – 4    

          Forma geral:
ax  = b,
em que x representa a variável (incógnita) e a e b são números racionais,   com a  0.
Dizemos que a e b são os coeficientes da equação.(ax = b, é a forma mais simples da equação do 1º grau)

          Exemplos:
        x – 4 = 2 + 7,  (variável x)
          2m + 6 = 12 – 3 ,(variável m)
        -2r + 3 = 31,   (variável r)
        5t + 3 = 2t – 1 ,  (variável t)
          3(b – 2) = 3 + b,(variável b)   

        4 + 7 = 11, (é uma igualdade, mas não possui uma variável, portanto não é uma equação do 1º grau)
        3x – 12 > 13, (possui uma variável, mas não é uma igualdade, portanto não é uma equação do 1º grau)

        Obs:

Devemos observar duas partes  em uma equação, o 1º membro à esquerda do sinal de igual e o 2º membro à direita do sinal de igual.

Veja: 

      Conjunto Universo: Conjunto formado por todos os valores que a variável pode assumir. Representamos pela  letra  U.

      Conjunto Solução: Conjunto formado por valores do conjunto U que tornam a sentença verdadeira.
Representamos pela letra  S.

Exemplo:

        Dentre os elementos do conjunto  F = {0, 2, 3, 6, 8, 9}, qual deles torna a sentença matemática
2x – 4 = 2,   verdadeira.
2(0) – 4 = 2 Errado
2(2) – 4 = 2 Errado
2(3) – 4 = 2 Verdadeiro

2(6) – 4 = 2 Errado

2(8) – 4 = 2 Errado

2(9) – 4 = 2 Errado

          Devemos observar que o conjunto U = {0, 2, 3, 6, 8, 9}, e conjunto S = {3}

Raiz da equação

        Um dado número é chamado de raiz da equação, quando este torna a igualdade verdadeira.

        Verificando se um dado número  é raiz da equação:

Exemplos:

          1. Vamos verificar se o número 4 é raiz da equação 9a – 4 = 8 + 6a Equação 9a – 4 = 8 + 6a

Vamos substituir a por 4  9(4) – 4 = 8 + 6(4)  36 – 4 = 8 + 24   32 = 32

Então, o número 4 é raiz da equação ou seja conjunto solução.

2.  Vamos verificar se o número – 3 é raiz da equação 2x – 3 = 3x + 2.

Vamos substituir x por – 3  2(-3) – 3 = 3(-3) + 2  – 6 – 3 = – 9 + 2  – 9 = – 7 , sentença  falsa
– 9 é diferente de –7 (- 9  – 7).

Então – 3 não é raiz da equação ou seja não é conjunto solução da equação.

Duas ou mais equações que possui o mesmo conjunto solução (não vazio) são chamadas equações  equivalentes.

        Exemplo:

          1. Dada as equações , sendo U = Q.

        x + 2 = 8,  a raiz ou solução  é = 6

          x = 8 – 2, a raiz ou solução é = 6

          x = 6, a raiz ou solução é = 6

          Podemos observar que em todas as equações apresentadas a raiz ou o conjunto solução é o mesmo. Por esse motivo, são chamadas equações equivalentes.

Resolvendo Equações do 1º grau

         Resolver uma equação do 1º grau em um determinado conjunto universo significa determinar a raiz ou conjunto solução dessa equação, caso exista solução.

        Resolução:

          Exemplo:

          Vamos resolver a equação 5a + 11 = – 4, sendo U = Q.

          Aplicando o principio aditivo, vamos adicionar –11 aos dois membros da equação, e isolar o termo que contém a variável a no 1º membro.

5a + 11 = – 4
5a + 11 + (– 11) = – 4 + (– 11) (adicionamos – 11 para podermos eliminar o + 11 do 1º membro)
5a + 11 – 11 = – 4 – 11 ( eliminamos os parenteses)
5a = – 15 (Quem está multiplicando a variável, passa para os 2º membro dividindo)

 S = {-3}

          obs:

        Se você prestou  atenção na resolução, deve ter observado que o número que estava em um membro com
determinado sinal aparece no outro membro com sinal diferente, e quem estava multiplicando  aparece
no outro membro dividindo. No processo prático fazemos assim.

          
Resolvendo equações pelo método prático:

Exemplos:

1) Resolva as seguintes equações do 1º grau com uma variável sendo
U = Q

a)  y + 5 = 8
y = 8 – 5     (+5 passou para o 2º membro – 5)
y = 3
S = {3}

b)  13x – 16 = – 3x
13x + 3x = 16   (- 3x passou para o 1º membro + 3x)
16x = 16    (16 estava multiplicando x, vai passar para o 2º membro dividindo)

x = 1
S = {1}

c) 3(x – 2) – (1 – x) = 13   (aplicamos a propriedade distributiva da multiplicação)

3x – 6 – 1 + x = 13

3x + x = 13 + 6 +1     (+6 e +1, passaram para o 2º membro – 6 e – 1)

4x = 20   (4 vai passar para o 2º membro dividindo)

x = 5
S = (5)

d)
 (tiramos o mmc)

5t –14 = 8t – 20  (cancelamos os  denominadores)

5t – 8t = -20 + 14

-3t = – 6 (multiplicamos por – 1, 1º membro é negativo)

3t = 6

t = 6/3

t = 2

S = {2}

2) Vamos resolver a equação  5x – 7 = 5x – 5, sendo U = Q.

5x – 7 = 5x – 5
5x – 5x = – 5 + 7
0x = 2

Não existe divisão por zero, dizemos que a equação é impossível  em Q, então S = { }(vazio).

3) Vamos resolver a equação 5x – 4 = – 4 + 5x.

5x – 4 = – 4 + 5x
5x – 5x = – 4 + 4
0x = 0

Dizemos que esta equação é indetermina (Infinitas soluções), logo S = Q.

4) Determine o conjunto solução da equação 18m – 40 = 22m, sendo U = N.

18m – 40 = 22m

18m – 22m = 40

 -4m = 40 (-1)

4m = – 40

m = – 10

Não existe – 10 no conjunto N(naturais), logo S = {  }.