Determinantes
Em matemática, determinante é uma função matricial que associa a cada matriz quadrada um escalar, ou seja, é uma função que transforma uma matriz quadrada em um número real. Esta função permite saber se a matriz tem ou não inversa, pois as que não têm são precisamente aquelas cujo determinante é igual a 0.
1) Considere as matrizes A = (aij) e B (bij) quadradas de ordem 2, com aij = 3i + 4j e bij = -4i – 3j. Sabendo que C = A + B, determine C2.
2) Calcule os seguintes determinantes:
a) ![]() b)
b) 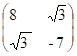 c)
c) 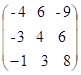
3) Se a = ![]() , b =
, b = ![]() e c =
e c = ![]() , determine A = a2 + b – c2.
, determine A = a2 + b – c2.
4) Resolva a equação ![]() = -6.
= -6.
5) Se A = ![]() , encontre o valor do determinante de A2 – 2ª.
, encontre o valor do determinante de A2 – 2ª.
6) Sendo A = 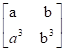 , calcule o valor do determinante de A e em seguida calcule o valor numérico
, calcule o valor do determinante de A e em seguida calcule o valor numérico
desse determinante para a = 2 e b = 3.
7) Calcule o valor do determinante da matriz A = 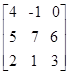
8) Resolva a equação 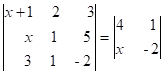
9) Se A = (aij)3×3 tal que aij = i + j, calcule det A e det At.
10) Foi realizada uma pesquisa, num bairro de determinada cidade, com um grupo de 500 crianças de 3 a 12 anos de idade.
Para esse grupo, em função da idade x da criança, concluiu-se que o peso médio p(x), em quilogramas, era dado pelo determinante da matriz A, em que: 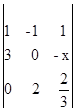 , com base na fórmula p(x) = det A, determine:
, com base na fórmula p(x) = det A, determine:
a) o peso médio de uma criança de 7 anos
b) a idade mais provável de uma criança cuja o peso é 30 kg.
11) Calcule o valor do determinante da matriz A= ![]() .
.
12) Resolva a equação ![]() = 3.
= 3.
13) Se A = ![]() , calcule o valor do determinante de
, calcule o valor do determinante de 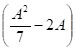 .
.
14) Considere a matriz A = (aij)2×2, definida por aij = -1 + 2i + j para ![]() .
.
Determine o determinante de A.
15) Determine o determinante da seguinte matriz 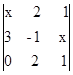 .
.
16) Dada a matriz A = 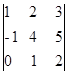 e a = det A, qual o valor de det (2A) em função de a?
e a = det A, qual o valor de det (2A) em função de a?
17) Seja A = (aij)3×3 tal que aij = i – j. Calcule det A e det At.
18) Calcule os determinantes das matrizes A = 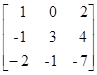 e B =
e B = 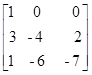 , usando o teorema de Laplace.
, usando o teorema de Laplace.
19) Resolva as equações:
a) ![]() = 0 b)
= 0 b) ![]() = 0 c)
= 0 c) ![]() = 0
= 0
20) Sabendo – se a = ![]() e b =
e b = ![]() , calcule o valor de 3a + b2.
, calcule o valor de 3a + b2.
21) Dada a matriz A = ![]() , calcule:
, calcule:
a) det A b) det A2
22) Determine o valor de cada determinante:
a) 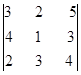 b)
b) 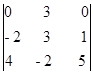 c)
c) 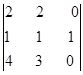
23) Calcule o determinante da matriz P2, em que P é a matriz P = 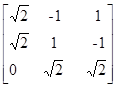 .
.
24) Na matriz 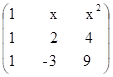 , calcule:
, calcule:
a) seu determinante
b) os valores de x que anulam esse determinante
25) Determine em IR a solução da equação: 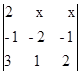 = 8 – log84.
= 8 – log84.
26) Sabendo que a = ![]() e b =
e b = 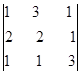 , efetue a2 – 2b.
, efetue a2 – 2b.
27) Determine a solução da equação: 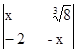 = 0.
= 0.
28) Determine o determinante da matriz ![]() .
.
29) Resolver a equação 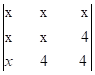 = 0
= 0
30) Resolva as equações:
a) 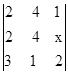 = 0 b)
= 0 b) 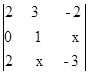 = 2 c)
= 2 c) 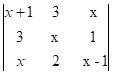 = 0
= 0


