Progressão aritmética (PA)
Progressão Aritméticas (PA)
É uma seqüência de números reais onde cada termo, a partir do segundo, é igual ao anterior mais uma constante ( chamada razão).
Exemplos:
Sendo a1 = 1 e a razão (r) = 2 então (a1 é o primeiro termo a2 o segundo termo e assim por diante)
a2 = a1 + r a2 = 1 + 2 = 3
a3 = a2 + r a3 = 3 + 2 = 5
a4 = a3 + r a4 = 5 + 2 = 7
an = an-1 + r (representação de um termo qualquer)
Assim a P.A. será (1, 3, 5, 7……)
Para calcularmos a razão de uma P.A. efetuamos a diferença entre um termo qualquer e seu anterior.
Exemplos:
Dada a P.A. (1, 4, 7, 10….)
r = 4 – 1 = 3; r = 7 – 4 = 3; r = 10 – 7 = 3
Termo Geral de uma P.A
Para calcularmos qualquer termo de uma P.A. usamos a fórmula seguinte:
|
an = a1 + (n – 1)r |
an = representa o termo procurado.
a1 = representa o primeiro termo da P.A
n = representa o número de termos.
r = representa a razão da P.A.
Exemplos:
1. Calcule o sétimo termo da P.A (1, 6, 11, …)
a7 = ? n = 7 a1 = 1 r = 6 – 1 = 5
an = a1 + (n – 1)r
a7 = 1 + (7 – 1)5
a7 = 1 + (6)5
a7 = 1 + 30
a7 = 31
Logo o sétimo termo desta P.A é 31.
2. Calcule o número de termos de uma P.A sabendo que a1 = – 14, an = 19 e r = 3.
an = 19 a1 = -14 r = 3 n = ?
an = a1 + (n – 1)r
19 = -14 + (n – 1)3
19 = -14 + 3n – 3
-3n = -14 -3 – 19
-3n = -36(-1)
3n = 36
n = 36/3
n = 12
Logo o número de termos é 12.
Propriedades
1ª = Sendo a, b, c três termos consecutivos de uma P.A, dizemos que o termo b central entre eles é a média aritmética dos outros dois.
Exemplo:
Sendo 2, x, 18 três termos consecutivos de uma P.A. Calcule o valor de x.
![]()
2ª = Numa P.A finita, a soma de dois termos equidistantes dos extremos é igual à soma dos extremos.
Exemplo:
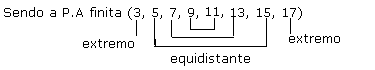
9 = 11 = 7 + 13 = 5 + 15 = 3 + 17 = 20
Formula da Soma dos Termos da P.A.
|
|
Sn= representa a soma dos termos da P.A.
a1 = representa o primeiro termo da P.A.
an = representa um determina termo da P.A.
n = representa um determinado número de termos da P.A.
Exemplos:
1. Calcule a soma dos 15 primeiros termos da P.A (8, 12, 16…)
s15 = ? a1 = 8 a15 = ? r = 12 – 8 = 4 n = 15
Observe que para usar a fórmula da soma primeiro devo calcular a15 .
an = a1 + (n – 1)r
a15 = 8 + (15 – 1)4
a15 = 8 + (14)4
a15 = 8 + 56
a15 = 64
![]()
![]()
Logo soma dos 15 temos é 540.
2. Sendo a1
= 0 e r = 2, calcule a soma dos 16 primeiros termos dessa P.A.
a1 = 0 r = 2 S16 = ? a16 = ?
an = a1 + (n – 1)r
a16 = 0 + (16 – 1)2
a16 = 0 + (15)2
a16 = 0 + 30
a16 = 30
![]()
![]()
Logo a soma dos 16 termos é 240.


