Matrizes

Matrizes

Definição
No século XVII o desenvolvimento da produção e do comércio colocou ao homem uma grande necessidade de trabalhar com tabelas numéricas.

O matemático inglês Arthur Cayley (1821 a 1895) aprofundou os estudos desses tipos de tabelas, e foi um dos primeiros a estudar e aplicar as matrizes em estruturas algébricas. Isto permitiu um grande desenvolvimento da Matemática.

Contudo, foram os chineses os grandes inventores das matrizes. Uma importante obra chinesa, escrita por volta de 250 a.C., intitulada ‘Nove Capítulos sobre a Arte Matemática’, nos mostra que os chineses, na solução de sistemas de equações, já utilizavam a ideia de matrizes.

Chamamos de matriz numérica a uma tabela de números, isto é, um conjunto de números colocados em linhas (horizontais) e em colunas (verticais). Entretanto, nem sempre ela será formada por números, podendo aparecer com
funções ou outras expressões matemáticas.

Em geral, denominaremos matriz de ordem m x n (lê-se m por n) a uma tabela de números formada por m linhas e n
colunas. As tabelas de números são escritas entre parênteses e são designadas por letras maiúsculas.

 

Assim, a matriz A é de ordem 3 x 4 (lê-se 5 por 3) e a matriz B de ordem 2 x 3 (lê-se 2 por 3).

Quando precisarmos expressar uma matriz qualquer, indicaremos cada um de seus elementos por uma
letra minúscula com subíndices que indicam a posição do elemento dentro da matriz. O primeiro número do subíndice indica a linha e o segundo número indica a coluna em que se encontra o elemento.

Assim, a₃₄ é o elemento de uma matriz que está na linha 3 e coluna 4.

A tabela abaixo, por exemplo, representa uma matriz qualquer de ordem 4 x 3.

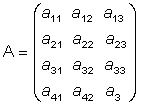
Podemos também expressar a matriz A, acima, de forma abreviada com a seguinte simbologia:

A = (a_ij); i = 1, 2, 3, 4; e j = 1, 2, 3

Como vimos: i  indica a linha e j assinala a coluna.

• Quando uma matriz tem apenas uma linha a chamamos de matriz linha. Sua ordem será 1 x n.

Exemplos: A = (1 2 -3)    B = (-3  8  7  -6)

• Quando uma matriz tem apenas uma coluna, denomina-se matriz coluna.
Sua ordem será m x 1.

Exemplos: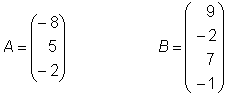

• Como as matrizes são tabelas de números, podemos nos deparar com uma matriz na qual todos os componentes sejam nulos. Elas são conhecidas como matrizes nulas.

Exemplos: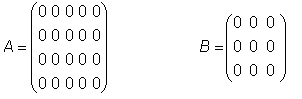

• Falaremos das matrizes transpostas. Diz-se que uma matriz é a transposta de A quando as linhas da transposta são as colunas de A.
A matriz transposta de A é representada por A’  ou A^t.

Exemplo: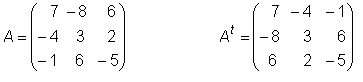

• Pode ocorrer também que a matriz tenha um mesmo número de linhas e colunas.
Estas são chamadas de matrizes quadradas de ordem n, em vez de matrizes de ordem n x n.

Nessas matrizes, os elementos da forma a_ij, como a₁₁, a₂₂, a₃₃
etc., formam o que se conhece como diagonal principal.

Exemplos:

• Dentro das matrizes quadradas cabe destacar aquelas que possuem todos os elementos nulos, com exceção dos correspondentes à diagonal principal.
São conhecidas como matrizes diagonais.

Exemplo:

• Numa matriz diagonal, quando todos os elementos da diagonal principal são iguais a 1, essa matriz receberá o nome de matriz identidade.

Exemplo:

Operações com matrizes

Soma de matrizes

Dadas as matrizes A e B de mesma ordem, definimos a operação soma de matrizes, A + B, como a nova matriz C que tem como elemento c_ij, na posição ij, a soma dos elementos a_ij + b_ij. Em outras palavras, todos os elementos da nova matriz C são obtidos aplicando-se
a seguinte expressão:

c_ij = a_ij + b_ij

Exemplo: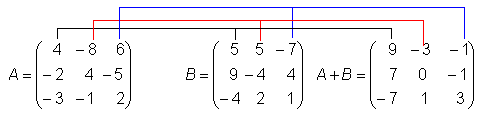

A soma de matrizes possui, assim como a soma de números, as seguintes propriedades:

• Propriedade associativa: A + (B + C) = (A + B) + C.
• Elemento neutro: é a matriz nula (0) correspondente.
• Elemento oposto: a matriz A tem por oposta –A
onde, se a A = (a_ij), então –A = (­ a_ij).

Produto de uma matriz por um número

Se tivermos um número Real m e uma matriz A = (a_ij) qualquer, definiremos o produto m X A como a matriz que tem
por componentes os elementos de A multiplicados por m, o que é o mesmo que m X A = (m X a_ij).

Exemplo: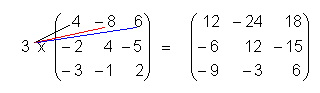

Um caso particular é o produto de: (­1) X A = A.
Com este produto obtém-se a matriz oposta A para qualquer matriz A.

Produto de matrizes
A multiplicação de matrizes só pode ser efetuada se o número de colunas da primeira matriz for igual ao número de linhas da segunda. Observe que a matriz-produto tem por ordem o número de linhas da primeira e o número de colunas da segunda.
O produto de uma matriz A de ordem m x n por uma matriz B de ordem n x p é uma matriz C, de ordem m x p, em que o elemento da linha c_ij é a soma dos produtos da linha i de A pelos  elementos correspondentes da coluna j de B.

Observe abaixo como fazemos a multiplicação entre matrizes:

Para obter o elemento da 2a. linha e 3a. coluna da matriz produto C=A.B, isto é, o elemento c(2,3), devemos:

1° = multiplicar os primeiros elementos da 2a. linha e 3a. coluna;

2° = multiplicar os segundos elementos da 2a. linha e 3a. coluna;

3° = multiplicar os terceiros elementos da 2a. linha e 3a. coluna;

4° = multiplicar os quartos elementos da 2a. linha e 3a. coluna;

5° = somar os quatro produtos obtidos anteriormente.(c₂₃ = a₂₁ b₁₃ + a₂₂ b₂₃ + a₂₃ b₃₃ + a₂₄ b₄₃)

Exemplo:
Dadas as matrizes A, de ordem 2 X 3, e B, de ordem 3 X 2, buscamos a matriz produto A X B, de ordem 2 X 2.