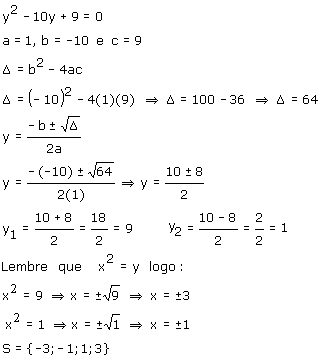Equações biquadradas
Você já estudou ao longo de sua vida escolar as equações de 1º grau, as equações de 2º grau agora chegou
a hora de aprendermos as equações biquadradas( Bi = duas vezes)
Definimos como equações biquadradas as equações escritas na seguinte forma:
|
ax4 + bx2 + c = 0 |
Exemplos:
|
x4 – 2x2 + 6 = 0 |
9x4 – 42x2 = 0 |
|
3x4 – x2 + 8 = 0 |
-x4 + 6 = 0 |
|
-7x4 – 5x2 + 8 = 0 |
-2x4 – x2 + 8 = 0 |
Obs: Note que nos exemplos temos equações biquadradas completas (quando possui todos os coeficientes numéricos) e
incompletas (quando falta um dos coeficientes numéricos b ou c, lembrando que o coeficiente a existirá sempre).
Resolvendo equações biquadradas
Vamos resolver a equação x4 – 10x2 + 9 = 0, observe que se trata de uma equação biquadrada x4 = (x2)2 , este está elevado ao quadrado duas vezes (biquadrada).
Vamos escrever a equação x4 – 10x2 + 9 = 0, da seguinte forma (x2)2 -10x2 + 9 = 0 observe que temos x2
duas vezes, vamos substitui-lo por y ou qualquer letra, sendo assim a nova equação será y2 -10y + 9 = 0.
|
|
Se você não entendeu a resolução dê uma olhada como se resolve uma equação do segundo grau usando a fórmula de Bhaskara.