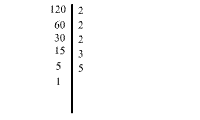Critérios de divisibilidade

     Um número é divisível por 4 quando termina em 00 ou quando o número formado pelos dois últimos algarismos da direita for divisível por 4.

Exemplo:
9500 é divisível por 4, pois termina em 00.
6532 é divisível por 4, pois 32 é divisível por 4.
836 é divisível por 4, pois 36 é divisível por 4.
9870 não é divisível por 4, pois não termina em 00 e 70 não é divisível por 4.

      Um número natural é divisível por 5 quando ele termina em 0 ou 5.Exemplos:
425 é divisível por 5, pois termina em 5.
78960 é divisível por 5, pois termina em 0.
976 não é divisível por 5, pois não termina em 0 nem em 5.

 
 
Divisibilidade por 6

      Um número é divisível por 6 quando é divisível por 2 e por 3 ao mesmo tempo.
Exemplos:
942 é divisível por 6, porque é divisível por 2 e por 3 ao mesmo tempo.
6456 é divisível por 6, porque é divisível por 2  e por 3 ao mesmo tempo.
984 não é divisível por 6, é divisível por 2, mas não é divisível por 3.
357 não é divisível por 6, é divisível por 3, mas não é divisível por 2.

Divisibilidade por 8

     Um número é divisível por 8 quando termina em 000, ou quando o número formado pelos
três últimos algarismos da direita for divisível por 8.

Exemplos:
2000 é divisível por 8, pois termina em 000.
98120 é divisível por 8, pois 120 é divisível por 8.
98112 é divisível por 8, pois 112 é divisível por 8.
78341 não é divisível por 8, pois 341 não é divisível por 8.

     Um número é divisível por 9 quando a soma dos valores absolutos dos seus algarismos for divisível por 9.

Exemplo:
6192 é divisível por 9, pois a soma de seus algarismos é igual a 6+1+9+2=18, e como 18 é divisível por 9, então 6192 é divisível por 9.

    Um número natural é divisível por 10 quando ele termina em 0.
Exemplos:
8970 é divisível por 10, pois termina em 0.
5987 não é divisível por 10, pois não termina em 0.

 Divisibilidade por 11

Um número é divisível por 11 quando a diferença entre as somas dos valores absolutos dos algarismos de ordem ímpar e a dos de ordem par é divisível por 11.
Exemplos:
87549
Si (soma das ordens ímpares) = 9+5+8 = 22
Sp (soma das ordens pares) = 4+7 = 11
Si – Sp = 22 – 11 = 11
Como 11 é divisível por 11, então o número 87549 é divisível por 11.439087
Si (soma das ordens ímpares) = 7+0+3 = 10
Sp (soma das ordens pares) = 8+9+4 = 21
Si – Sp = 10 – 21
Como a subtração não pode ser realizada, acrescenta-se o menor múltiplo de 11 (diferente de zero) ao minuendo, para que a subtração possa ser realizada: 10+11 = 21. Então temos a subtração 21-21 = 0.
Como zero é divisível por 11, o número 439087 é divisível por 11.

     Um número é divisível por 12 quando é divisível por 3 e por 4.
Exemplos:
1200 é divisível por 12, porque é divisível por 3  e por 4 ao mesmo tempo.
870 não é divisível por 12 é divisível por 3, mas não é divisível por 4.
8936 não é divisível por 12 é divisível por 4, mas não é divisível por 3.

    Um número é divisível por 15 quando é divisível por 3 e por 5 ao mesmo tempo.
Exemplos:
9105 é divisível por 15, porque é divisível por 3  e por 5 ao mesmo tempo.
9831 não é divisível por 15 é divisível por 3, mas não é divisível por 5.
680 não é divisível por 15 é divisível por 5, mas não é divisível por 3.

Números
primos são os números naturais divisíveis apenas por 1 e ele mesmo.      

  Exemplos:
2   tem apenas os divisores 1 e  2, portanto  2 é  primo.
       23 tem apenas os divisores 1 e 23, portanto 23 é primo.
       10 tem os divisores 1, 2, 5 e 10, portanto 10 não é  primo.       

Atenção:
  
1 não é um número primo, porque ele tem apenas um divisor  ele mesmo.
  
2 é o único número primo que é par.
  Os números que têm mais de dois divisores são chamados números compostos.
Exemplo:
36  tem mais de dois divisores então 36 é um número composto.

Existe um dispositivo prático para fatorar um número. Acompanhe, no exemplo, os passos para montar esse
dispositivo: